- Autora Matthew Elmers elmers@military-review.com.
- Public 2023-12-16 21:58.
- Última modificació 2025-01-24 09:20.

En aquest article, intentarem determinar la durabilitat de les armadures russes de la Primera Guerra Mundial. Aquesta qüestió és extremadament difícil, ja que està molt poc tractada a la literatura. I la qüestió és aquesta.
És ben sabut que a finals del segle XIX, les principals potències marítimes en la construcció de vaixells de guerra van passar a l’armadura fabricada pel mètode Krupp. Però això no vol dir en absolut que des de llavors l'armadura dels vaixells de tots aquests països s'hagi convertit en equivalent.
El cas és que la "recepta clàssica" de l'armadura de Krupp (també coneguda com a "qualitat 420", creada el 1894) no va romandre inalterada, sinó que va millorar. Almenys per països com Anglaterra i Alemanya. Però, fins a quin punt es va perfeccionar a si mateix i fins a quin resultat van arribar els amos de les armadures de diversos poders: això, per desgràcia, no ho sé del cert.
Prova per foc
La resistència als projectils de l'armadura russa es pot determinar amb una precisió acceptable, gràcies al bombardeig experimental de l'antic cuirassat "Chesma", reclassificat com a "buc exclòs núm. 4". Es va crear un compartiment experimental al vaixell, que copiava la protecció de diverses parts dels dreadnoughts de la classe de Sebastopol i, per a la puresa de l’experiment, també es va equipar amb molts dispositius que haurien de tenir aquestes parts. Així, per exemple, s’instal·laven a les casamates canonades de vapor (que hi passaven en cuirassats), armes de foc, dispositius de control de foc i cables elèctrics, etc.

Després, el compartiment experimental es va disparar amb diverses municions de calibre de 6 a 12 polzades, incloent, per descomptat, les últimes petxines de 305 mm per perforar l’armadura i explosius. Dit això, els informes de proves són molt complets, com hauria de ser en aquests casos. Contenen no només una descripció de les conseqüències d’un cop, sinó també la velocitat del projectil en el moment en què impacta contra l’armadura, així com l’angle en què es troben el projectil i l’armadura.
Tot plegat ens permet calcular la resistència de les armadures russes en relació amb les últimes closques domèstiques de 470, 9 kg, segons la mateixa fórmula de Jacob de Marr, que he citat diverses vegades anteriorment. Però ho tornaré a citar, de manera que el benvolgut lector no hagi de revisar els articles anteriors. La proporció de la qualitat del projectil i la durabilitat de l'armadura en aquesta fórmula es descriu pel coeficient "K". A més, com més elevat sigui aquest coeficient, més forta serà l’armadura.

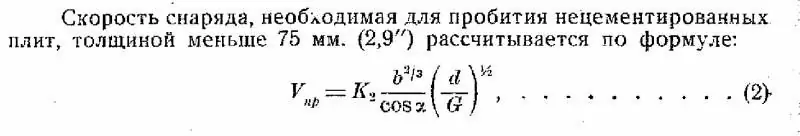
Una certa dificultat a l’hora d’avaluar l’armadura russa es crea pel fet que es van provar principalment les petxines i no la resistència definitiva de la protecció dels darrers dreadnoughts. Sembla ser: quina diferència hi ha? Però, de fet, és molt significatiu. Quan s’estan provant els projectils, l’interès està en la seva destrucció fiable d’armadures a les principals distàncies de batalla. Quan es prova l’armadura, hi ha interès en les condicions finals en què encara pot protegir el vaixell.
Tot i això, les estadístiques d'èxits del "vaixell exclòs núm. 4" encara ens permeten treure certes conclusions.
Quant a disparar amb armadura de 250 mm
Malauradament, els cops de blindatge de 125 mm o menys no ens interessen; en tots els casos va resultar que l’energia del projectil era més que suficient per penetrar-hi o els angles d’impacte eren tan petits que donaven una rebotjar. En altres paraules, per determinar la durabilitat de les armadures, les estadístiques de cops sobre armadures de 125 mm o inferiors no serveixen de res.
Una altra cosa és colpejar la gruixuda armadura de 225 mm i 250 mm, que veurem de prop.
Comencem amb 250 mm d’armadura, que protegia les parets de la torre de comandament del "vaixell exclòs núm. 4". En total, es van disparar 13 trets contra aquesta timoneria, però alguns es van disparar contra el seu sostre i altres per mitjà de bombes explosives. Les petxines perforadores van ser disparades a una armadura de 250 mm només 5 vegades.
El tret més potent va ser el número 6 (numerat segons els informes de proves). Un projectil perforador de 305 mm va xocar contra la placa de l'armadura amb un angle de 80 ° (10 ° respecte al normal) a una velocitat de 557 m / s. Un projectil tindria una velocitat similar de 470,9 kg a una distància de només 45 cables. És cert que l’angle de desviació respecte a la normal seria inferior a 6, 18 °.
Per descomptat, la closca va perforar l’armadura. Per mantenir-la, caldria una armadura amb una "K" superior a 2.700, i això és un valor desorbitat, fins i tot segons els estàndards de l'armadura molt més avançada de la Segona Guerra Mundial. Els càlculs fets per mi mostren que, a distància, el mod de pistola rus de 305 mm / 52. El 1907 va poder penetrar la placa blindada de "qualitat 420" de 433 mm de Krupp.
Els 4 trets restants es van disparar en igualtat de condicions. La velocitat del projectil a l’armadura era de 457 m / s, els angles de trobada amb l’obstacle eren d’uns 80 ° (desviació dels 10 ° normals). Segons els meus càlculs, les petxines russes tindrien una velocitat tal a una distància de 75 cables, però l’angle de trobada amb un obstacle seria pitjor: 76, 1 ° (desviació de la normal: 13, 89 °). En aquestes condicions, segons els càlculs anteriors, van penetrar 285,7 mm d'armadura Krupp (amb K = 2000). Però, en realitat, tot no va resultar tan inequívoc.
Durant el tret número 11, tot va anar sense problemes. La perforadora va superar la placa blindada de 250 mm, va impactar contra la paret oposada de la timoneria i va explotar i va fer un forat en el punt d’impacte de 100 mm de profunditat. Quan es va disparar el número 10, l'armadura també es va trencar. Però no està del tot clar quan es va produir exactament l'esclat de la closca; això no s'indica a l'informe. Però, pel que sembla, això va passar a l'interior de la torre de comandaments, perquè la força de l'explosió va arrencar les plaques d'armadura del terrat i la placa adjacent de 250 mm simplement es va arrencar dels muntatges i es va desplegar.

Així, amb aquest tret, s’hauria de comptar la penetració i el pas net del projectil per a la protecció de l’armadura en el seu conjunt.
Però quan es va disparar el número 9, es va produir un petit incident: la petxina va impactar contra l'armadura just davant del terra de 70 mm. Com a resultat, la placa blindada de 250 mm es va perforar i fins i tot la seva cantonada, d’aproximadament 450x600 mm, es va trencar i es va trobar un forat de 200 mm de llargada al terra de 70 mm. Per tant, es pot argumentar que també en aquest cas el projectil no només va perforar l’armadura, sinó que ho va fer amb una quantitat d’energia decent, que va ser suficient per danyar una xapa d’acer blindada de 70 mm situada horitzontalment.
En conseqüència, en quatre de cada cinc cops, els obusos russos perforants van mostrar el resultat esperat, confirmat pels càlculs segons de Marr. Però quan es va disparar el número 7, va passar una cosa estranya: el projectil va colpejar la placa de l'armadura exactament de la mateixa manera, amb el mateix angle de 80 ° i amb la mateixa velocitat de 457 m / s, però no va perforar l'armadura, explotant durant el seu pas. Com a resultat, va resultar un forat amb una profunditat de 225-250 mm: només hi entraven "fragments d'un projectil de fins a 16 kg de pes".
Veiem que de 4 cops de petxines perforadores de 305 mm, que haurien d’haver penetrat en les armadures de més de 285 mm de gruix, només 3 eren penetracions “netes”. En un cas, la closca va explotar mentre passava per l’armadura, tot i que hauria de no ho ha estat.
Quin és el motiu d’aquest fracàs? Potser és la pròpia closca? Suposem que un fusible defectuós ha funcionat prematurament. Però també és possible una altra interpretació: el fet és que la penetració de l’armadura per un projectil té un caràcter probabilístic. És a dir, no hi ha tal cosa que, per exemple, si, segons la fórmula de Jacob de Marr, el gruix màxim de l’armadura travessada per un projectil en determinades condicions és de 285 mm, l’armadura de 286 mm no es penetrarà pel projectil en qualsevol cas. Pot trencar-se. I viceversa: trencar en les mateixes condicions contra una armadura de gruix menor.
Dit d’una altra manera, la pròpia fórmula de Jacob de Marr (o qualsevol altra anàloga a la mateixa) no té gens de precisió farmacològica. En realitat, hi ha rangs sencers en què un projectil que colpeja una placa blindada amb un angle determinat i a una determinada velocitat pot penetrar a l’armadura amb un cert grau de probabilitat, però això no es pot calcular utilitzant fórmules de penetració d’armadura generalment acceptades. I pot ser que en el cas del tret núm. 7 la probabilitat esmentada hagi funcionat.
Per tant, al meu entendre, els resultats del tret número 7 són aleatoris i no s’han de tenir en compte. I l'armadura dels dreadnoughts russos amb un gruix de 250 mm no va poder suportar ser impactada per 470, 9 kg d'un projectil a una velocitat de 457 m / si un angle de trobada amb un obstacle d'uns 80 °. Segons De Marr, resulta que el coeficient "K" de l'armadura russa en aquest cas hauria de ser inferior a 2.228. Però quant?
Al meu parer, la resposta es pot obtenir analitzant les conseqüències del tret núm. 11. La ronda va perforar una placa de 250 mm, va colpejar la paret oposada i hi va fer un forat de 100 mm. Per tant, podem suposar que la penetració màxima de l’armadura del projectil rus de 470,9 kg amb els paràmetres anteriors era de 250 mm de l’armadura cimentada de Krupp. I 100 mm addicionals d’armadura homogènia sense cimentar separada.
Per què és homogeni? El cas és que, com ja sabeu, l’armadura cimentada consisteix, per dir-ho així, en dues capes. La superior és molt forta, però alhora fràgil, i després comença una armadura més suau, però més viscosa. El projectil, que va colpejar la placa blindada de 250 mm, va colpejar la capa "suau i viscosa" des de l'interior de la timoneria, que per les seves qualitats és bastant similar a una armadura homogènia en lloc de cimentada.
A més, s'ha de tenir en compte que estic calculant el coeficient "K" d'un projectil que passa a través de l'armadura en el seu conjunt i que explota darrere d'ella. Però en el cas del tret núm. 11, això no va passar: la closca, que va trencar 250 mm de l'armadura cimentada de Krupp i va colpejar la part posterior de la segona placa, no va perforar l'armadura, sinó que va explotar i només va tenir en compte tenint en compte l'energia de l'explosió, va aconseguir fer un sot de 100 mm. Per tant, el càlcul de "blindatge homogeni de 250 mm cimentat + 100 mm" es pot considerar basat en supòsits que òbviament són desfavorables per a l'armadura. En conseqüència, el resultat obtingut es pot considerar el mínim per sota del qual no tindrà la resistència de l’armadura Krupp de fabricació russa.
I llavors el càlcul és molt senzill. La velocitat del projectil, com s’ha dit moltes vegades més amunt, és de 457 m / s, l’angle de desviació del normal quan toca la placa blindada de 250 mm és de 10 °. En passar per aquesta armadura, el projectil "girarà" i colpejarà la segona placa ja amb un angle de 90 °, és a dir, 0 ° de desviació de la normal. Això es desprèn del diagrama núm. 9 "" Curs de tàctica naval. Artilleria i Armadures "L. G. Goncharov, donat a la pàgina 132. On, a més de la força de les petxines a l’impacte, hi ha un gràfic del gir de la petxina en passar per l’armadura, en funció de l’angle de trobada amb aquesta armadura.
La relació de resistència de les armadures de les armadures homogènies i cimentades russes és desconeguda per a mi. Però, segons G. Evers, l'armadura cimentada alemanya tenia un coeficient "K" un 23% superior a l'homogeni. I, probablement, per a l’armadura russa, aquesta proporció també és certa. A més, cal tenir en compte que en passar per una placa blindada de 250 mm, el projectil perdrà la seva tapa perforadora. Això, al contrari, provocarà un augment de l'armadura homogènia "K" en un 15%.
En calcular la velocitat d'un projectil per penetrar en una placa homogènia de 100 mm, es va utilitzar la mateixa fórmula que per a una placa cimentada de 250 mm, només es va canviar el coeficient "K". Sé que L. G. Goncharov va recomanar utilitzar una fórmula diferent donada al seu llibre de text per a una armadura homogènia. Però, segons ell, està dissenyada per a plaques d'armadura més fines de 75 mm. Tenim, al cap i a la fi, 100 mm. A més, segons G. Evers, l'ús de la fórmula anterior de Jacob de Marr també és aplicable per a armadures homogènies.
Segons els resultats del càlcul de la "K" de les armadures russes cimentades, el 2005 té un valor. Ara anem a veure si hi ha hagut casos durant el tir que refutessin aquest resultat.
Quant a disparar amb una armadura de 225 mm
Només es van disparar 2 tirades de petxines perforadores contra l’armadura de 225 mm. A més, la velocitat del projectil en el moment del contacte amb l’armadura era de fins a 557 m / s, tal velocitat que el projectil hauria d’haver tingut a una distància de 45 cables. És cert que l’angle de trobada amb l’armadura era molt desavantatjós: 65 ° o 25 ° desviació de la normal. Però fins i tot en aquest cas, per suportar l'impacte de 470,9 kg del projectil, la placa d'armadura hauria de tenir un coeficient "K" superior a 2 690. El que, per descomptat, és completament impossible. Dit d’una altra manera, quan es disparava amb aquests paràmetres, fins i tot l’armadura de l’era de la Segona Guerra Mundial s’havia de perforar amb un enorme subministrament d’energia del projectil.
I amb el tret número 25, això va passar exactament. La carcassa va perforar fàcilment la placa de blindatge de 225 mm (ni tan sols es va trencar, sinó que va trencar-ne un tros de 350x500 mm) i va colpejar el bisell, que consistia en una armadura de 25 mm sobre un metall de 12 mm. substrat i hi va fer un forat de 1x1, 3 m. No s’ha establert la ubicació exacta de l’esclat del projectil. Però es va suposar que va entrar a la sala de màquines i ja va explotar allà. En altres paraules, el resultat va ser exactament el que hom podria esperar amb aquest cop.
Però amb la segona ronda (pla núm. 27), tot va resultar incomprensible. El projectil es va desviar del punt d’objectiu. I, com diu l'informe, "colpeja la vora superior de l'armadura". El resultat de la presa serà més fàcil de citar del document:
“El projectil va fer un forat a l’armadura d’uns 75 mm de profunditat i uns 200 mm d’amplada i, arrencant la vora que sobresortia de la camisa amb un quadrat, va explotar sense frenar aquí, desprenent fum negre. La casamata núm. 2 no ha estat danyada.
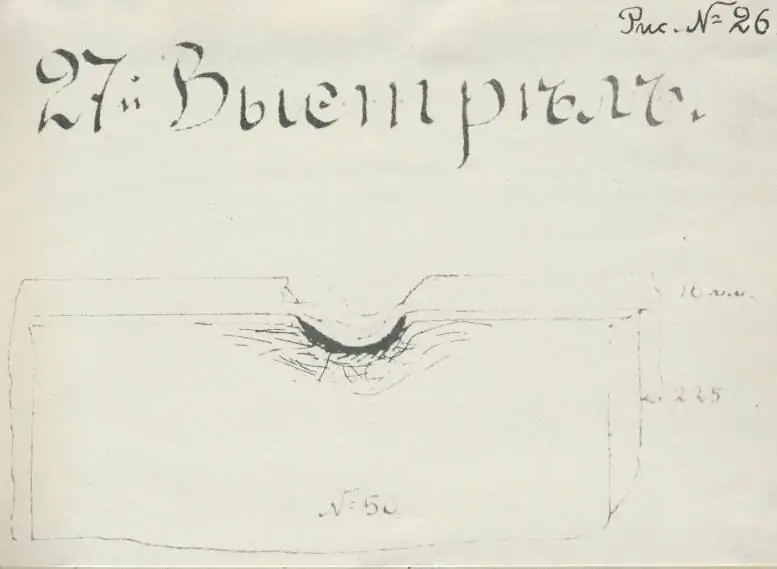
No està completament clar què podria haver passat aquí. Principalment perquè no està clar on va colpejar exactament la closca. Per començar, "vora" és un concepte extensible, ja que es pot utilitzar, entre altres coses, per significar "la vora d'alguna cosa". És a dir, ni tan sols queda clar si la línia central del projectil va colpejar la superfície vertical o horitzontal de la placa blindada.
Però, en presència d’un fusible d’alta qualitat, s’esperaria un dany molt més gran en qualsevol d’aquestes opcions. Si el projectil va colpejar el pla vertical de l'armadura, hauria d'haver col·lapsat a la seva profunditat màxima, no en 75 mm. Si l’impacte va caure sobre la part horitzontal, llavors, per què, doncs, s’inclou l’angle de l’obstacle que es troba a uns 65 ° a l’informe? El projectil no va caure del cel sobre la superfície horitzontal de la llosa de 225 mm, es va disparar amb un angle de 65 ° respecte a la superfície vertical, el que significa que hauria d’haver estat de 25 ° respecte a l’horitzontal. En aquest cas, podeu esperar un rebot. O (en cas d’explosió d’un projectil) dany a la coberta de blindatge horitzontal de 37,5 mm adjacent a la vora superior de la placa de blindatge de 225 mm. Però res d’això va passar.
Al meu parer, la falla va ser un projectil defectuós que es va esfondrar a l’impacte, motiu pel qual l’explosió no va resultar amb tota la seva força. O, potser, un fusible defectuós que va detonar "explosius" en el moment en què el projectil va tocar l'armadura. També és possible que el projectil no fos defectuós, sinó que es va esfondrar perquè l'angle format per les dues superfícies de la placa blindada tenia el paper d'una mena de "trinxador". Formalment, el projectil no va penetrar a les plaques de 225 mm. Però, en relació amb l'extrema inusualitat de les conseqüències del cop, al meu entendre, no s'ha de buscar la raó en les qualitats ultra altes de la placa blindada.
En conseqüència, els resultats de bombardejar les plaques blindades de 225 mm del "vaixell núm. 4 exclòs" no confirmen ni refuten la nostra conclusió anterior.
No obstant això, hi va haver altres proves emblemàtiques de petxines i armadures domèstiques que van tenir lloc el 1920. Aquí l'objectiu era completament diferent. El compartiment experimental es va construir sota el Pare Tsar per determinar l’esquema de protecció òptim per als futurs dreadnoughts russos. Però el 1917, alguna cosa va fallar amb l’autocràcia a Rússia. I els projectes per a la construcció de dreadnoughts han passat a la categoria de projectar. No obstant això, es van dur a terme proves, incloses les utilitzacions de petxines de 305 mm 470, 9 kg. Els resultats són molt interessants. Però en parlarem al següent article.
Però el que voldria assenyalar per separat és la presència d’una estranya curiositat a les proves. El fet és que van sobreestimar deliberadament les distàncies del foc d’artilleria.
Així, per exemple, per a trets a armadures de 225 mm amb obusions perforades, s’indica que la distància corresponent als paràmetres de l’obstacle és de 65 cables. Però això no és cert: a una velocitat de 557 m / s amb una desviació de la normal de 25 °, un projectil de 305 mm hauria d’haver penetrat a l’armadura un 8% més gruixut que quan es disparava a 65 cables, on la velocitat del projectil seria han estat 486,4 m, i la desviació de la normal - 10, 91 °.
Per descomptat, es pot sospitar d’un error banal en els càlculs de l’autor de l’article, és a dir, jo. Però, doncs, com s’entén el tir a la torre de comandament (aquí es mostra la velocitat del projectil de la mateixa manera que la velocitat del projectil és de 557 m / s desviació de la normal) només a 10 °, però la distància es considera la mateixa, és a dir, 65 cables? ! En altres paraules, resulta que la "distància adequada" es va indicar sense tenir en compte l'angle d'incidència, només en termes de velocitat del projectil?
Tanmateix, aquesta versió es pot verificar fàcilment. Segons els meus càlculs, la velocitat del projectil per a 60 cables és de 502,8 m / s i per a 80 cables és de 444 m / s. Al mateix temps, les dades sobre el llançament de canons de 305 mm / 52 donades per L. G. Goncharov ("Curs de tàctica naval. Artilleria i armadura", p. 35), mostra per a aquestes distàncies 1671 i 1481 ft / s, respectivament, traduïdes al sistema mètric: 509 i 451 m / s.
Per tant, podem suposar que la meva calculadora encara produeix un cert error cap avall, que ascendeix a 6-7 m / s. Però és obvi que 557 m / s per a 65 cables i 457 m / s per a 83 cables estan fora de qüestió aquí.
I un fet més que et fa pensar. Com podeu veure, es van disparar un total de 7 llançaments de petxines perforadores de 305 mm contra una armadura de 225-250 mm. Al mateix temps, les condicions de tir eren tals que l’armadura especificada va haver d’obrir-se amb un marge considerable. No obstant això, en condicions reals de tir, fins i tot a distància, només en cinc casos de set obus van perforar l'armadura. I només van passar 4 petxines a l'interior.






