- Autora Matthew Elmers [email protected].
- Public 2023-12-16 21:58.
- Última modificació 2025-01-24 09:21.

Què determina la precisió: una de les característiques principals d'una arma? Viouslybviament, per la qualitat del barril i del cartutx. Posposem el cartutx per ara, però considerem la física del procés.
Agafeu una vareta o tub metàl·lic de metall elàstic i fixeu-lo rígidament en una base massiva. Així doncs, obtenim un model del dispositiu en estudi. Ara, si colpejem la vareta, no importa en quin lloc i en quina direcció, ni tirar-la cap enrere, ni prémer-la, o, finalment, introduir un cartutx al tub i disparar un tret, veurem que la vareta (barril) ha entrat en un moviment oscil·latori amortit. Aquestes vibracions es descomponen en les més simples i cada tipus de vibració tan simple del canó afectarà la precisió (precisió) del tir a la seva manera.
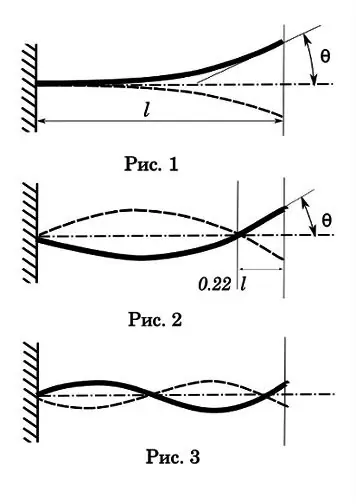
Comencem per les vibracions de primer ordre o de to. Com podeu veure (figura 1), aquesta oscil·lació només té un node al punt de fixació, l'amplitud més gran, el temps de desintegració més llarg i el temps d'oscil·lació més llarg d'un període. Aquesta vegada és de 0,017-0,033 seg. El temps de recorregut de la bala a través del forat és de 0, 001-0, 002 seg. És a dir, significativament inferior al cicle d’una oscil·lació, cosa que significa que aquest tipus d’oscil·lació no té un efecte significatiu sobre la precisió d’un sol tret. Però amb el rodatge automàtic, pot resultar una imatge interessant. Diguem que la velocitat de foc és de 1200 rds / min, és a dir, temps d'un cicle: 0,05 seg. Amb un període d’oscil·lació de primer ordre de 0, 025 segons, tenim una relació de freqüència múltiple. I aquesta és una condició indispensable per a la ressonància amb totes les conseqüències que se’n deriven: l’arma comença a tremolar amb tanta força que es pot desfer.
Passem a les oscil·lacions del segon ordre (figura 2). Però suggereixo que els estudiants d’humanitats primer facin un experiment per eliminar les mancances de l’educació en el camp de la física. Cal agafar un nen petit (es pot una noia), posar-lo en un gronxador i gronxador. Abans tens un pèndol. Poseu-vos al costat del gronxador i intenteu colpejar el noi amb la pilota. Després d'una sèrie d'intents, arribareu a la conclusió que la millor manera de colpejar és quan l'objectiu es troba en la primera fase d'oscil·lació: la desviació màxima del punt d'equilibri. En aquest punt, l'objectiu té velocitat zero.
Vegem el diagrama de segon ordre. El segon node de vibració es troba aproximadament a 0,22 del final del canó. Aquest punt és una llei de la naturalesa, és impossible crear aquestes vibracions per al feix voladís de manera que el segon node caigui a l’extrem lliure. És on és i no depèn de la longitud del canó.
L’amplitud de l’oscil·lació per a l’esquema de segon ordre és menor, però el temps d’oscil·lació ja és comparable al temps de pas de la bala a través del forat - 0, 0025-0, 005 seg. Per tant, per al rodatge individual això ja és d’interès. Per deixar clar de què parlem, imagineu-vos un barril d’1 metre de llarg. La bala recorre tot el barril en 0, 001 segons. Si el període d’oscil·lació és de 0,004 s, al moment en què la bala surt del barril, el barril assolirà el seu màxim revolt a la primera fase. La pregunta per a les humanitats és: en quin moment (en quina fase) és millor llançar una bala fora del barril per garantir la coherència dels resultats? Recordeu el swing. En el punt zero, el vector de la velocitat de deflexió del tronc és màxim. És més difícil que una bala toqui aquest punt al tall del barril, també té el seu propi error de velocitat. És a dir, el millor moment perquè la bala surti volant serà quan el canó estigui al punt més alt de la primera fase de deflexió, com a la figura. Aleshores, desviacions insignificants en la velocitat de la bala es compensaran pel temps més llarg que el barril ha passat en la seva fase més estable.
Una representació gràfica d’aquest fenomen es pot veure clarament al diagrama (figura 4-5). Aquí: Δt és l’error temporal amb què la bala creua el morrió del canó. A la fig. 4 és ideal quan el temps mitjà d’enlairament de bala coincideix amb la fase zero de l’oscil·lació del barril. (Matemàtics! Sé que la distribució de la velocitat no és lineal.) L'àrea ombrejada és l'angle de propagació de les trajectòries.
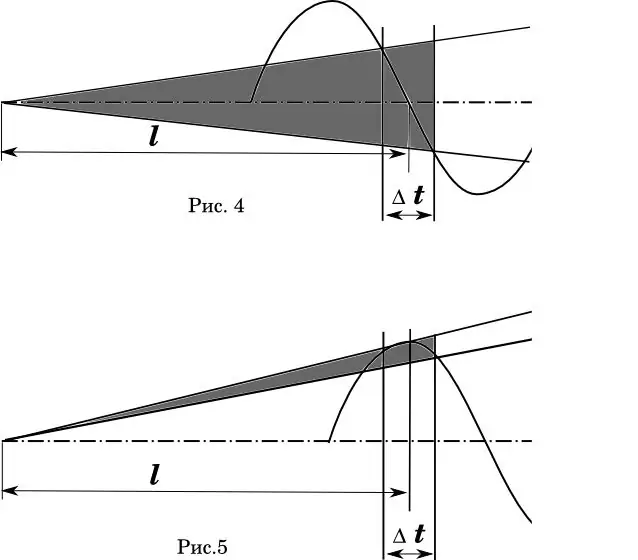
A la figura 5, la longitud del canó i l’error de velocitat continuen sent els mateixos. Però la fase de flexió del barril es desplaça de manera que el temps mitjà de sortida coincideix amb la màxima deflexió del barril. Els comentaris són superflus?
Bé, val la pena l’espelma? Quina gravetat poden tenir les desviacions causades per oscil·lacions de segon ordre? Greus i molt greus. Segons el professor soviètic Dmitry Aleksandrovich Ventzel, en un dels experiments es van obtenir els següents resultats: el radi de la desviació mitjana va augmentar un 40% amb un canvi de la longitud del canó només de 100 mm. En comparació, un processament de barrils d’alta qualitat només pot millorar la precisió en un 20%.
Vegem ara la fórmula de la freqüència de vibració:
on:
k - coeficient per a oscil·lacions de segon ordre: 4, 7;
L és la longitud del barril;
E és el mòdul d’elasticitat;
I és el moment d'inèrcia de la secció;
m és la massa del tronc.
… i procediu a l'anàlisi i conclusions.
La conclusió òbvia de les figures 4-5 és un error de velocitat de bala. Depèn de la qualitat de la pols i del seu pes i densitat al cartutx. Si aquest error és com a mínim una quarta part del temps del cicle, es pot renunciar a tota la resta. Afortunadament, la ciència i la indústria han aconseguit una estabilitat molt gran en aquest tema. I per als més sofisticats (per exemple, en reposabanca) hi ha totes les condicions per a l’autoassemblatge de cartutxos per ajustar exactament la fase d’alliberament de la bala a la longitud del canó.
Per tant, tenim un cartutx amb la variació de velocitat més baixa possible. La longitud del barril es va calcular en funció del seu pes màxim. Sorgeix la qüestió de l’estabilitat. Observem la fórmula. Quines variables afecten el canvi en la freqüència d'oscil·lació? Longitud del canó, mòdul d’elasticitat i massa. El barril s’escalfa durant la cocció. Pot canviar la longitud del canó de manera que la precisió es vegi afectada. Sí i no. Sí, ja que aquesta xifra es troba a centèsimes de percentatge per a una temperatura de 200 C. No, ja que el canvi del mòdul elàstic de l’acer per a la mateixa temperatura és d’aproximadament un 8-9%, per a 600 ° C és gairebé el doble. És a dir, moltes vegades més alt! El canó es torna més suau, la fase de flexió del canó avança en el moment en què surt la bala, la precisió baixa. Bé, què diu un analista reflexiu? Dirà que és impossible obtenir la màxima precisió en una longitud de barril en mode fred i calor. L'arma pot tenir un millor rendiment amb un canó fred o calent. En conseqüència, s’obtenen dues classes d’armes. Una és per a accions d’emboscada, quan s’ha de colpejar l’objectiu des del primer tret "fred", perquè la precisió del segon serà pitjor a causa de l’inevitable escalfament del barril. En aquesta arma no hi ha necessitat urgent d’automatització. I la segona classe són els rifles automàtics, la longitud del canó dels quals s’ajusta al canó calent. En aquest cas, un possible error a causa de la poca precisió d'un tret en fred es pot compensar amb un tret ràpid i més precís posterior.
EF Dragunov coneixia molt bé la física d’aquest procés quan dissenyava el seu rifle. Us proposo que us familiaritzeu amb la història del seu fill Alexei. Però primer, algú haurà de trencar-se el cervell. Com ja sabeu, dues mostres de Konstantinov i Dragunov es van apropar a la final de la competició per a un rifle de franctirador. Els dissenyadors eren amics i es van ajudar mútuament en tot. Per tant, el rifle de Konstantinov estava "ajustat" al mode fred, el rifle de Dragunov a "calent". Intentant millorar la precisió del rifle del rival, Dragunov dispara el seu rifle amb llargues pauses.

Vegem de nou la fórmula. Com podeu veure, la freqüència també depèn de la massa del barril. La massa del tronc és constant. Però el contacte dur amb el front produeix una retroalimentació positiva imprevisible al barril. El sistema - barril-forend-arm (suport) tindrà un moment d'inèrcia diferent (un conjunt de masses en relació amb el punt de fixació), el que significa que això també pot provocar un desplaçament de fase. És per això que els atletes utilitzen un suport suau. La mateixa característica s’associa amb l’aplicació del principi de “canó suspès”, quan el front de l’arma no té un contacte dur amb el canó i s’hi fixa rígidament (l’arma) només a la zona del receptor, i el segon extrem no toca en absolut el canó o bé toca a través d’una junta amb molla (SVD).
Pensament final. El fet que amb la mateixa longitud de canó sigui impossible obtenir la mateixa precisió a diferents temperatures proporciona una excel·lent raó per estirar el cervell. Només cal canviar la longitud i / o la massa del canó quan canvia la temperatura del canó. Sense canviar ni la longitud ni el pes del canó. Des del punt de vista de les humanitats, això és una paradoxa. Des del punt de vista d’un tècnic, una tasca ideal. Tota la vida d’un dissenyador està relacionada amb la solució d’aquests problemes. Els Sherlocks descansen.






